こんにちは、ガチ目に忙しくなったら自然とスマホのクソゲーに割く時間が激減したすのえです。
ちょっと暇になった時に軽く手を出せてしまうスマホのゲームって割と存在が罪ですよね。
自分は、暇なときにはマインスイーパーをやっています。ハマりすぎず、すぐやめれますし。
まあ、私がマインスイーパーが好き好き人間というのはアイコンからも伝わる通りですよね。

そんなある日、普通にマインスイーパーをしていたら「ヤバい」盤面を引いてしまいました。
せっかくなので数学Aの観点からこの盤面が出現する確率を求めたいと思います。
※注意※
この記事は、数学が得意でない人間の行う精一杯な数学的考察で構成されています。
ミスを見つけても怒らないでください。そして、出来たらコメントかTwitterのDMで優しく教えてください。
ヤバい盤面を引いた
さんざんヤバいと謳い尽くした盤面、こちらです。右がスクショ、左がそれを拡大したものです。
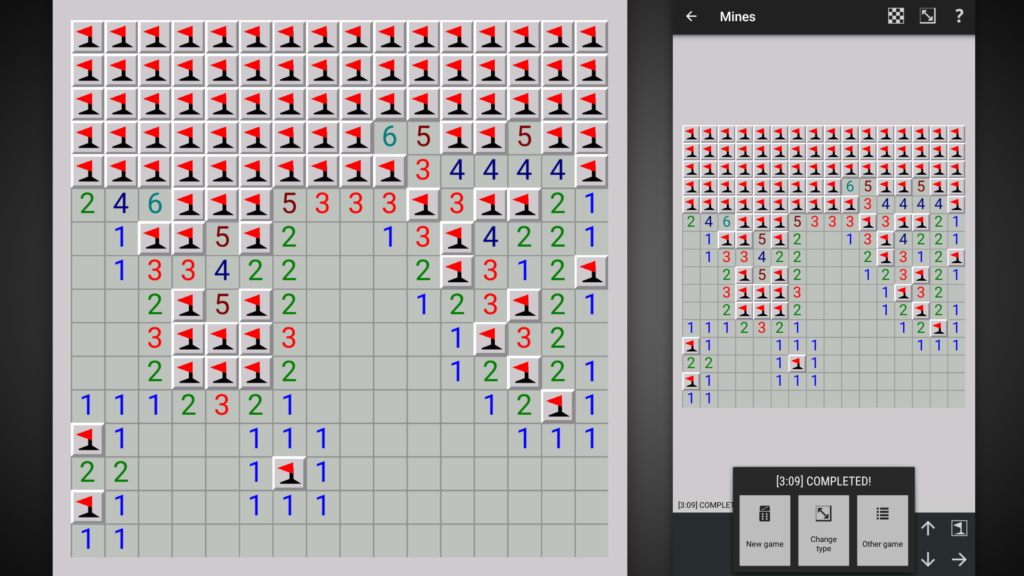
環境も一応述べておきます。使用OSはAndroid12。
Androidアプリ「Simon Tatham’s Puzzles」の「Mines」の「16×16, 99 mines」モードです。
(というかこのアプリは本当に良いです。パズルの種類が多いし広告がない。素晴らしいです。Slant好き。)
上から4行目の「6 5 5」の部分を開ける前にスクリーンショットもしていて、
「この中から3つ開けるのかよwww」というツイートをするつもりだったんですよ。
でも整理したら4行目右に3つ空きがあると分かって。「えじゃあ上の三行何…?」で結果がこれ。
これ奇跡だよね? おかしいよね? そうでもないのかな? 分からん、誰か助けて状態でした。
ということでこの盤面がどのくらいの確率で起きるのか確かめたくなりました。


一枚目のスクショを取った時に盤面の異常さに気付いて焦り散らかし、
地雷を5つ発見するのに50秒かかっていることが分かりますね。ワロタ
※注意※
本項以降では、高校数学やプログラミングを使用した確率の評価を行います。
お急ぎの方、数学が苦手な方などは >まとめ< に直接飛んでしまうことを推奨します。
そもそもマインスイーパーって?
マインスイーパーを知らない方へ、興奮のあまり説明を忘れていた私の愚かさを詫びておきます。
マインスイーパーとは、隠された地雷(マイン)を全て除去(スイープ)するゲームです。
最初プレイヤーには何も書かれていないマスのみで構成された碁盤状の盤面が渡されます。
プレイヤーはマスを開くことができ、マスには地雷があるものとそうでないものがあります。
開いたマスに地雷が無かった場合、その周辺3×3マスにある地雷の数を知ることができ、
地雷が入ってるものを開いてしまえばその場でゲームが終了してしまいます。
空マスのヒントを活用し、空マスを全て開けることができれば勝ち、というゲームです。
それでこの盤面の何がすごいのか、ということは何となくお分かりいただけると思います。
地雷はコンピュータによってランダムに設置されます。それがあの整頓具合。奇跡ですよね。
ちなみにヒントなしの一発目で地雷を引きゲームが終了する理不尽を防ぐため、
最初に開いたマス周辺3×3は空きマスであることが確定しているのが基本のようです。
このアプリでは、「プレイヤーがタップした瞬間に盤面が生成される」仕様らしく、
自分が始めるマスが一つでもズレていたらこの盤面にはならなかったかも。やっぱ奇跡だよね?
確率を考えよう
直感的に奇跡なこの盤面が本当に奇跡かどうかは、数学的な計算で検証する必要があります。
勉強ができない私ですが、高校の確率を頑張って思い出しながら確率を求めたいと思います。
盤面の状況
この盤面の確率を評価するために、まずは「この盤面の何がすごいのか」を具体的にします。
私がこの盤面を奇跡と感じた理由は、下の二つです。
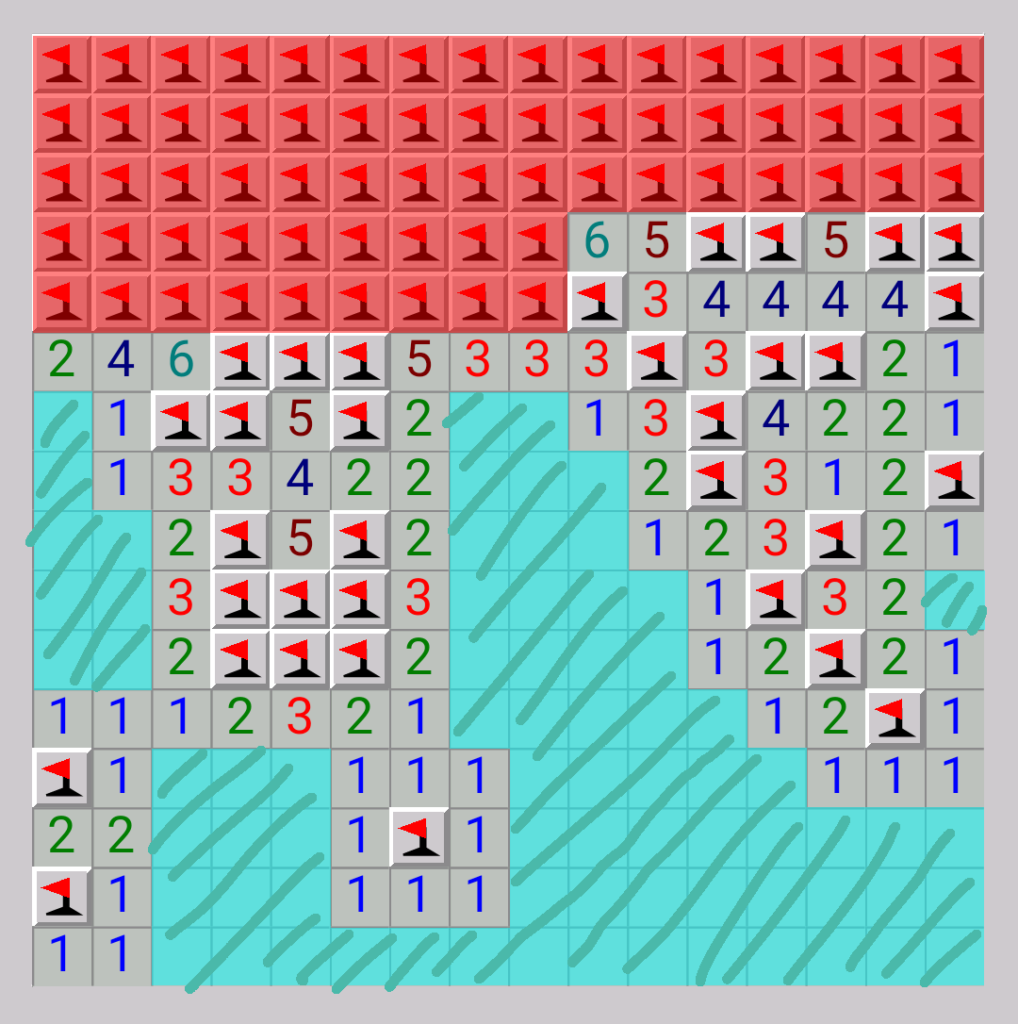
- 99個中66個の地雷が綺麗に配置されている点。
- 256マス中74個のマスが地雷非隣接である点。
こんなものでしょう。順に確率を求めていきます。
確率:66個の地雷が綺麗に配置される
一つ目の奇跡の可能性、「66個の地雷が綺麗に配置される」の可能性を考えてみます。
まず、「綺麗」とは何でしょうか?
この「綺麗」は以下の2要素に分けて考えることができると思います。
- 上寄せかつ左寄せである。
- くぼんだ領域が矩形(長方形)、かつ高さが2以下である。
右寄せより左寄せを美しいと感じるのは使用している言語が左横書きだからでしょうか。
では、「綺麗」の定義を行ったところで確率の考察に入りましょう。
綺麗を数学的に言い換える
まず、純粋に考えると「256マスの中から99個中66個が指定した66マスにある」確率ですが、
実はマインスイーパーの性質上最初に開けたマスの周辺9マスは空きが確定します。
そのため、実際は「247マスの中から99個中66個の地雷が指定した66マスにある」確率であり、
また「148個の空マスが247マス中指定した171マスに分布する」と言い換えることが可能です。
(256-99=157個が空きマスですが、9個は初期で空きが確定し、157-9=148個ですね。分布域も同様です。)
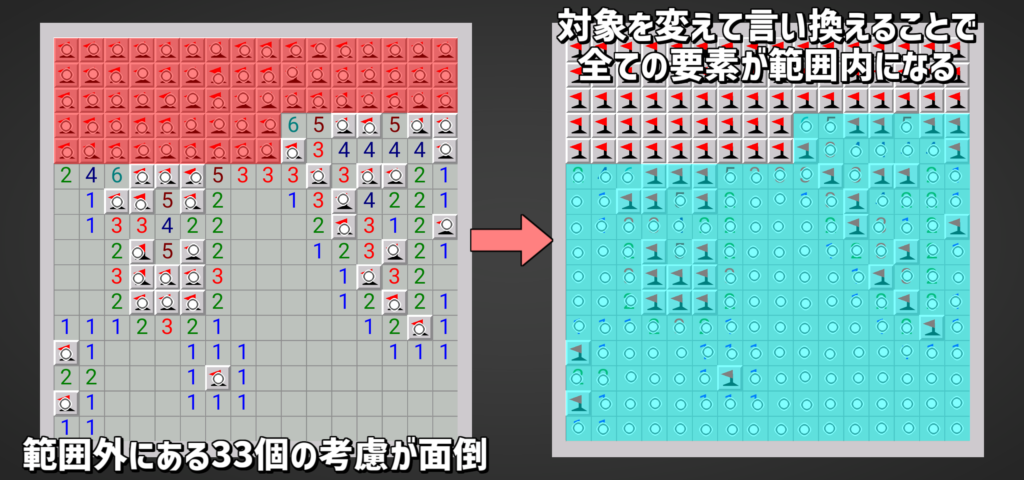
このような事象を\(M_a\)と置きましょう。しかし、計算前にまだ前提を考える必要があります。
例えば、「100枚中、一等が5枚、二等も5枚のくじ」があったとしたとき、
引いて二等が当たったらその事は「5%の確率」と言うべきではないと思いませんか?
5%の確率で一等が当たるなら、「二等以上が当たる確率は10%」とした方が正しくないですか?
つまり、「66の地雷が左上寄せかつ高さ2の矩形状のくぼみがある」よりも強い幸運があるなら
その確率も足した方が「綺麗になる確率」としては正しいと感じました。これも考慮します。
「綺麗さ」は曖昧さを含む
では「66の地雷が左上寄せかつ高さ2の矩形状のくぼみがある」よりも強い幸運とは何か。
それは、「66の地雷が左上寄せかつ高さ1の矩形状のくぼみがある」ですよね。
そしてそれは、\(M_a\)と同様の計算にて確率を求めることができます。
一部の人は、「67以上の地雷」の場合も「より強い幸運だ!」と感じたかもしれません。
ですが確率に加算できるのは、その幸運が他から影響されない場合に限るのではないでしょうか。
先ほど挙げたくじの例を使うと、一等の中に1枚特賞が混じっていたとしても、
「一等以上が当たる確率は 5+1 %」ではないですよね?
67以上の地雷が左上寄せかつ高さ2矩形くぼみで存在する確率は、\(M_a\)の確率を内包します。
そのため、地雷の数が増えたときの綺麗さの確率は加算する必要がないと考えています!
計算
以上より、今回の「綺麗さ」以上の地雷の配置を見れる確率は、\(2 P(M_a)\)と分かりました。
今後のため、「今回の綺麗さ以上の地雷の配置がされる事象」は\(M_A\)と置きましょう。
あ、重ねて言いますがこれは考察であり、私は数学が苦手なので間違っていら連絡お願いします。
「~~でした(キリッ」とかやって違ったらヤバいです。正しいと信じて計算を再開します。
\[ P(M_A) = 2 P(M_a)= 2 \times \frac{181}{247} \times \frac{180}{246} \times \cdots \times \frac{34}{100} = 2 \prod_{i=1}^{148} \frac{182-i}{248-i} \]
「総乗」という、総和\(\Sigma\)の積バージョンを使用しています。なんとなく分かれ。
にしても計算量膨大すぎるでしょ。コンピュータの力を借ります。機械は偉大。
結果は、「\(3.7325239597160127070926548\cdots \times {10}^{-35}\)」でした。
…
つまり、\(1 / 2.68 \times 10^{34}\)、「約“268溝”分の1」…ということです。
コイントスで言うなら、114回連続表が出る確率程度の奇跡です。(\(2^{114} \approx 2.07\times10^{34}\))
え???? 嘘だよね!?!?!???
僕明日死んじゃうよ!?!?!?!?
助けてください。 しかもまだもう一つの奇跡が残っています。かなりヤバいです。
あせらず計算していきましょう。
確率:74個のマスが地雷非隣接となる
今度は二つ目の奇跡の可能性、「74マスが地雷非隣接となる」確率を求めていきましょう。
まず、「地雷非隣接」とは、周囲3×3マスのどこにも地雷が存在しない、ということです。
つまり、1マス1マスを考えるのではなく、盤面全体を俯瞰して考えなければいけないのです。
この確率は高校で習う数学で太刀打ちすることができません。非常に困りました。
ですが、一つ目の奇跡(確定)の時の思考方法でこれを解決する着想を得ています。
再び先ほどの5枚の一等と5枚の二等の存在する100枚くじを考えてみてください。
くじの中身を知らない人が、他の人から「二等以上が当たる確率は10%」と聞いたとします。
すると知らない人でも、「一等に当たる確率は10%より低い」と当然わかることでしょう。
つまり、「知りたい事象を内包するより緩い事象の確率」を知れれば、それ以下だと分かります。
もう奇跡は一つ目で十分です。死にそうなんですよ。緩い確率でも大体で分かればいいです。
「より緩い事象」の確率
ではより緩い事象とは何でしょうか。出来たら緩すぎる事にはしたくありません。
ここで再び例の画像について空きマスの方に着目してカウントをしてみたところ、
「地雷非隣接マス」と「地雷非隣接マスを囲む空きマス」の和は74+55=129マスでした。
つまり、「129マスの密集した空きマスによって74マスの地雷非隣接マスが生成された」訳です。
これについて、空きマスが密集するためには地雷も他所に密集しなければなりませんよね。
地雷の密集が生成される確率は低いので、地雷がより散乱して密集した空きマスが減った状況は、
密集した空きマスが多い状況よりも確率が厳しいと言えるのではないでしょうか!?
つまり次の図のような状態を指しています。なんとなく理解してください!
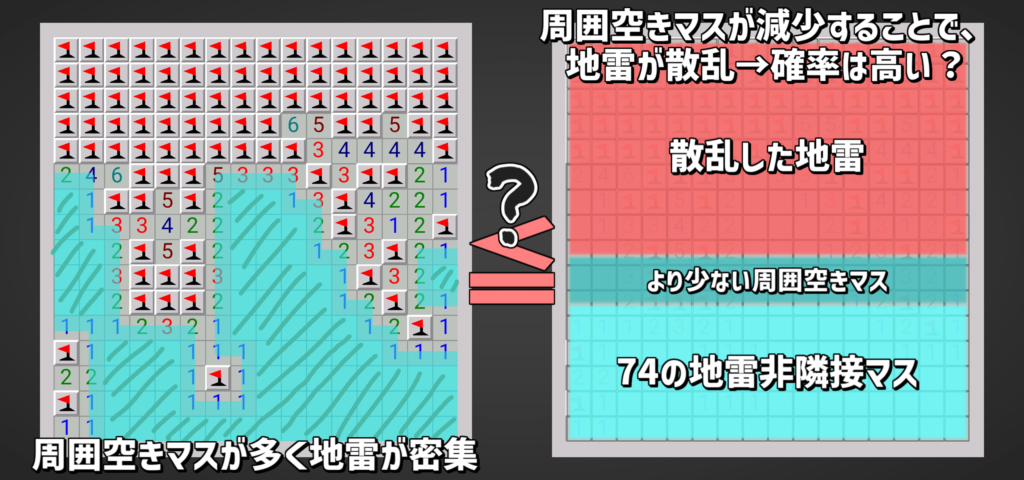
地雷非隣接マスが密集するのも確率が低そうという指摘は無視します。
次の項でここでの予想確率を使用せず両方の事象が同時に起こる確率を導出するので。(ネタバレ)
ここでは、「発想次第で物事は簡単になり、数学が生かせる」という話がしたいだけです。
「密な空きマス」から考える
地雷非隣接マスとそれを囲む空きマスを合わせて「密な空きマス」と呼ぶことにしましょう。
試しに並べてみたところ、地雷非隣接マスが74の時の密な空きマスの最小数は91マスです。
そのうち9マスはプレイヤーの初期マスによって生成されますから、言い換えると…
二つ目の事象は「99の地雷が247マスの中から指定の148マスに分布する」より確率が低いかも!
ということになります。確かではないですが、まあまあな分析ができるんじゃないでしょうか。
計算
二つ目の事象を\(M_b\)と置くと、先ほどの仮定より以下の計算式が立ち、確率を評価できます。
\[ P(M_b) \leq \frac{148}{247} \times \frac{147}{246} \times \cdots \times \frac{50}{149} = \prod_{i=1}^{99} \frac{149-i}{248-i} \]
再び機械の力を借りて計算をしてもらいます。結果は…
「\(5.13016743918556418906932933\cdots \times {10}^{-32}\)」でした。
…
つまり、\(1 / 1.95 \times 10^{31}\)、「“1950穣”分の1」…ということです。
コイントスで言うなら、104回連続表が出る確率くらいですかね。(\(2^{104} \approx 2.02\times10^{31}\))
ッフヒw ブハハハハハwwwww
マインスイーパーおもしろwwwwwwwwwwwww(??????)
確率:二つの事象が同時に起こる
では最後に、二つの事象が同時に起こる可能性を考えていきましょう。
もう勉強のことを考えすぎて頭がパンクしそうです。でも続けますよ。
もしこの二つの事象が「独立した事象」なら純粋に掛け算をすれば求めることができます。
ですが先ほども述べた通り、「地雷が密集する」ことと「地雷非隣接マスが多い」ことに
高い正の相関関係があることは容易に予想がつくことでしょう。つまり二つは独立していません。
では二つの事象が同時に起こる確率の限りない低さを数学的に示すことはできないのでしょうか?
いいえ、我々にはまだ「統計を利用した手法」が残されています!!!
そういえば自分は少しだけプログラミングをかじっていたことを思い出しました。
プログラミングを延々回して統計データを作れば、任意の確率を得ることができます。
二つが独立した事象でないなら、片方の事象を条件付きにして独立させれば良いのです!!
一つ目の奇跡の確率には割と自信があるので、二つ目の奇跡(多分)の確率を置き換えましょう。
一つ目の奇跡が起きたという条件の上でさらに二つ目の事象が起きる確率のデータを作ります。
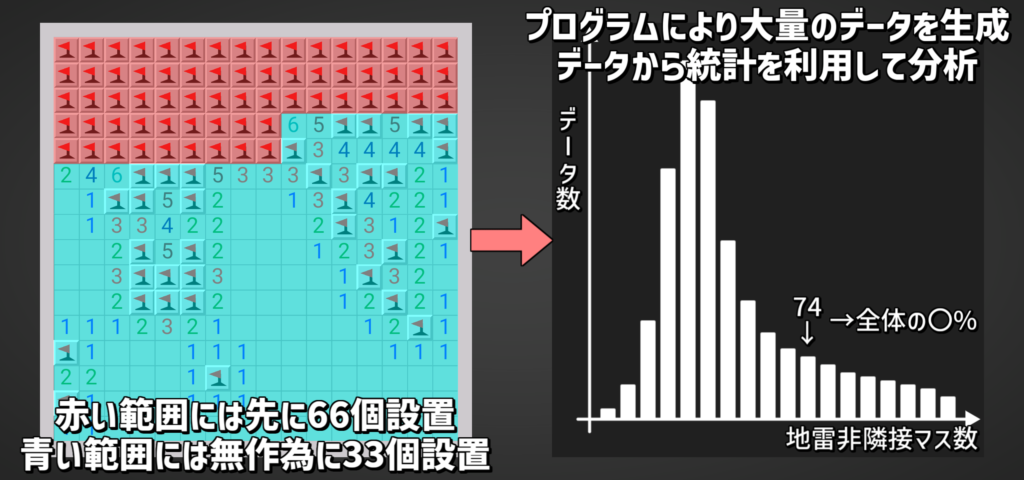
この図のようにすれば確率が分かるはずです!ということで頑張ってプログラムを作りました。
リポジトリを置いておきます。プログラミング初心者なので、好きに覗いて叱ってください。
適当にリポジトリを作りました:snoe1024/ms_board_counter
データの生成
図で簡単に説明しましたが、上には二つのプログラムが置いてあり、それぞれ
- n回の試行中、一つ目の奇跡(高さ2の矩形)条件で二つ目の事象以上が起きる回数を出力
- n回の試行中、一つ目の奇跡(高さ1の矩形)条件で二つ目の事象以上が起きる回数を出力
を得ることができます。
二つ目の事象でも一つ目の奇跡と同様、「地雷非隣接マスが74超過」も確率に含めていきます。
そうでないと限定されて小さくなった確率が私を精神的に殺してきますからね。怖すぎる。
とりあえずどちらも1億回試行してデータを出してみます。これだけやれば十分でしょ。
6.5万個のデータを出すのに30秒かかったので、単純計算で14時間かかると思います。おやすみ~
生成結果
ms_board_counter/ main.py [Final Data] over73: 308 / 100000000 - from prob_LMb_1 ms_board_counter/ sub.py [Final Data] over73: 234 / 100000000 - from prob_LMb_2
以上のような結果になりました。
ついでで地雷非隣接マスの数の統計も取ったので、そちらもグラフで出しておきます。
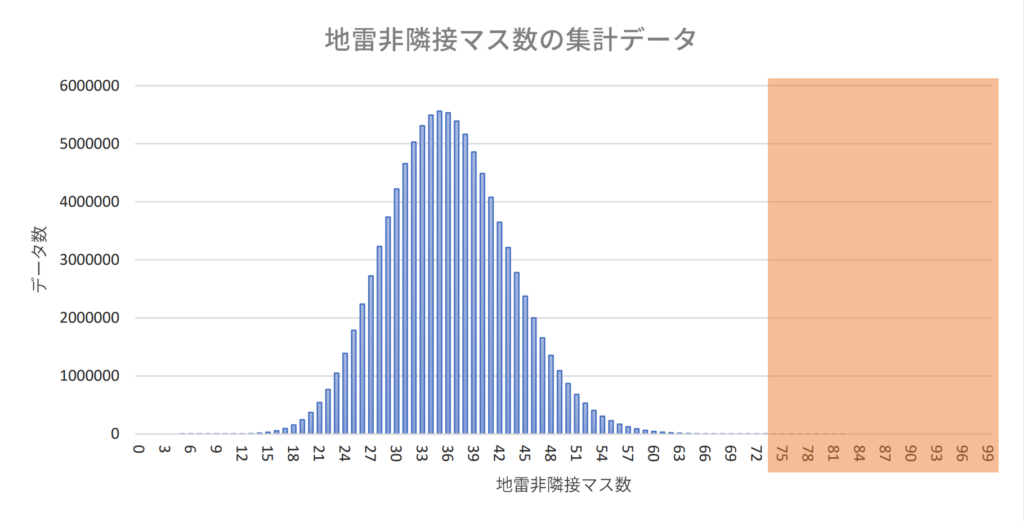
赤くした部分が、地雷非隣接マスが74個以上出現したデータ数を示している場所です。
せっかくなので、「対数グラフ」という縦軸が特殊なグラフも用意しました。
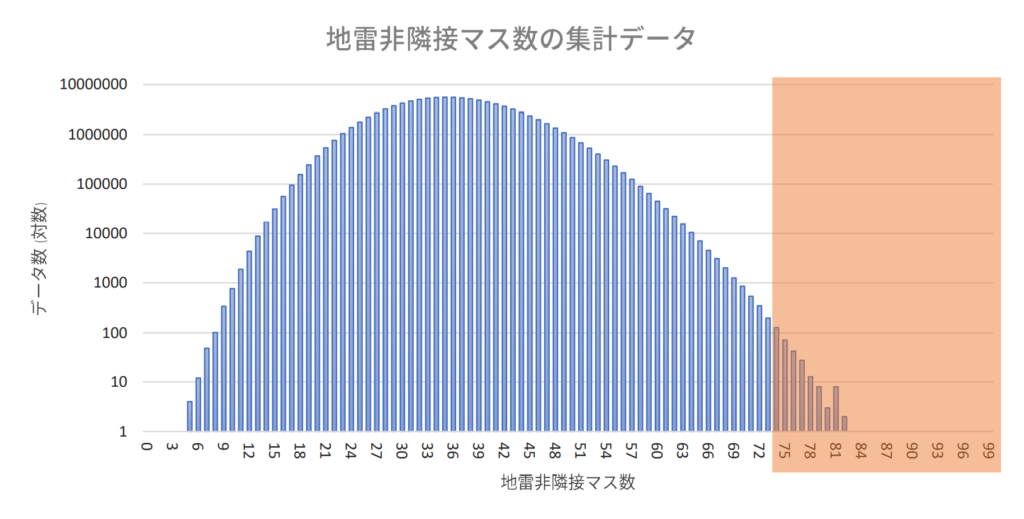
対数グラフは、縦方向に棒が伸びたときの増加速度が一定でなく、
横に引かれた線一本分長くなると数が10倍になる、という特徴を持つグラフです。
大きいデータと小さいデータの差が膨大な場合に使用するらしいです。初めて使いました。
この結果から簡単に事象\(M_b\)の条件付き確率を評価すると、
「一つ目の奇跡が100万回起きても、その盤面に地雷非隣接マスが74個以上あるのは2,3回」
ということになります。
計算
地雷非隣接マスが74個以上存在する事象を\(M_B\)と置いたとき、
\[ P(M_A \cap M_B) = P(M_a) \times 308 / {10}^{8} + P(M_a) \times 234 / {10}^{8} = \frac{1}{2} P(M_A) \times 542 \times 10^{-8}\]
によって今回の二つの事象が同時に起こる可能性を予想することができ、結果は
\(1.0115139930830394\cdots \times 10^{-40} \)、つまり「約“1正”分の1」になります。
コイントスと比べると、133回連続表が出る確率と同じくらいらしいです。(\(2^{133} \approx 1.09 \times {10}^{40}\))
なんか… もう驚けなくなってきたというか… これが本当に現実で起きたのか…
あの記憶とスクリーンショットが本当に正しいのか自分が信じられなくなってきました。
まとめ
16×16, 地雷数99のマインスイーパーにて私が今回偶然引いた盤面の出現確立を考察したところ、
まず、「66個の地雷が綺麗に配置される」、またはそれ以上の事象が発生する確率\(P(M_A)\)は
\[ P(M_A) = 2 \prod_{i=1}^{148} \frac{182-i}{248-i} = 3.7325\cdots \times {10}^{-35}\]
より約“268溝”分の1(\( 1 / 2.68 \times 10^{34} \))であるということが分かりました。
さらに、「74マスが地雷非隣接となる」またはそれ以上の事象が併発する確率\(P(M_A \cap M_B)\)は
\[ P(M_A \cap M_B) =\frac{1}{2} P(M_A) \times 542 \times 10^{-8} = 1.01151\cdots \times 10^{-40}\]
より約“1正”分の1(\( 1 / 9.89 \times 10^{39} \approx 1 / 10^{40} \))であるということが分かりました。
感想
まさか日々の暇つぶしで\(1 / 10^{40}\)を引けてしまうなんて。ハハ。
いや~~~~~~~~~~…
良い人生でした!!!!!
でも…
もうちょっと望みを言うとするなら…
年収2500万円くらい稼げる日本人になりたかった!!!!
(割合:\(1 / 2.87 \times 10^{3} \) 資料:令和元年度分 民間給与実態統計調査 – 国税庁)
IQ170くらいの人間になってみたかった!!!!
(割合:\(1 / 6.41 \times 10^{5} \) 標準偏差想定:ウェクスラー式)
年末ジャンボ宝くじで一等の七億円当てたかった!!!!!
(確率:\(1 / 2.0 \times 10^{7} \))
麻雀で天鳳・国士無双十三面待ちとか決めたかった!!!!!!
(確率:\(1 / 2.27 \times 10^{10}\) 引用:みのっちのブログ様)
なんでマインスイーパーでこの確率出せちゃったんでしょうか。
この確率って要するに、
全人類(\(7.8\times 10^{9}\))が、一年で平均一万回(\(1\times 10^{4}\))マインスイーパーをするとして、
そんな文明が今から100万年(\(1\times 10^{6}\))続いた惑星がこの銀河に1000万個(\(1\times 10^{7}\))あって、
そんなキモイ銀河が全宇宙に1億個(\(1\times 10^{8}\))あったとしても、
合計試行回数は\(7.8 \times 10^{34}\)回ですから…
僕はこれから一生マインスイーパーのアイコンで暮らすべきなのかもしれませんね。
あとそう、極めて確率の低い幸運に恵まれた人「明日俺死ぬ」って言いがちですけど、
確率は収束する、の言葉に沿って行くと確率の低い出来事は続けて起こらないと思うんですよ。
もしかしたら今後、自分は一生平凡な生涯を送ることになるんじゃないでしょうか…
ということで皆さん、マインスイーパーをプレイするときは気を付けてください。
そして、これと同じような盤面に遭遇した方は私にご連絡ください!!待ってますから!!!
さて、私は「どうせただの合成画像だろ」とか言ってくる人を見返すために、
もう一度似たような盤面が出るまで出られない世界に行くボタンを押そうと思います。
名付けて「一正回ボタン」なんてどうでしょう。 記憶は無くなりませんけどね!



コメント